[Concurrent Queue] 並發隊列

在這個 AI 的時代，大多數的資料結構或演算法可以很容易透過 AI 生成。但我發現 lock-free 演算法/資料結構是個例外，AI 的生成結果經常會有 deadlock 產生，所以我打算自己試著把常見的資料結構改成 Concurrent 的形式。

我自己沒有寫註解的習慣，程式碼中所有註解是 AI 加上去的。測試我也只讓 AI 隨意生成測試程式而已，但邏輯上應該沒問題，如果有人能幫我測過我會很感激的。

[The radix-2 Cooley-Tukey FFT / FNTT Algorithm] 庫利-圖基 快速 (傅立葉/數論) 變換演算法

離散捲積 (Discrete Convolution)

給定兩個數列 $A = (a_0, a_1, \dots a_{n-1}),\ B = (b_0, b_1, \dots, b_{m-1})$，
求兩數列的離散捲積 $C = (c_0, c_1, \dots, c_{n+m-2})$，其中 $$c_k = \sum_{i + j = k}a_ib_j$$

我們可以將數列轉換成多項式： 

$$\begin{align} A(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}\\B(x)=b_0+b_1x+b_2x^2+\dots+b_{m-1}x^{m-1}\end{align}$$

這樣一來，$c_i = (A * B)(x)$ 在 $x^i$ 項的係數，如果用最 naive 的做法，總共要花 $O(n\times m)$ 的時間。
這裡的目標是要在 $O((n+m)\log (n+m))$ 的時間算出 $C$。

多項式的表示法

係數表示法 Coefficient Representation

對於一個 $n-1$ 次多項式 $F(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}$，
我們可以用 Coefficient Representation 來表示他：

$F(x) := [a_0, a_1, \dots, a_{n - 1}]$

點值表示法 Point-value Representation

除此之外，令 $x_0, x_1, \dots, x_{n-1}$ 為 $n$ 個不同的數字，
我們也能用這些點在 $F$ 中的取值來表示他

令 $y_i = F(x_i),\ i = 0, 1, \dots, n-1$，
則 $F(x):= [y_0, y_1, \dots, y_{n - 1}]$

這種表示法又叫做 Point-value Representation

新的思路

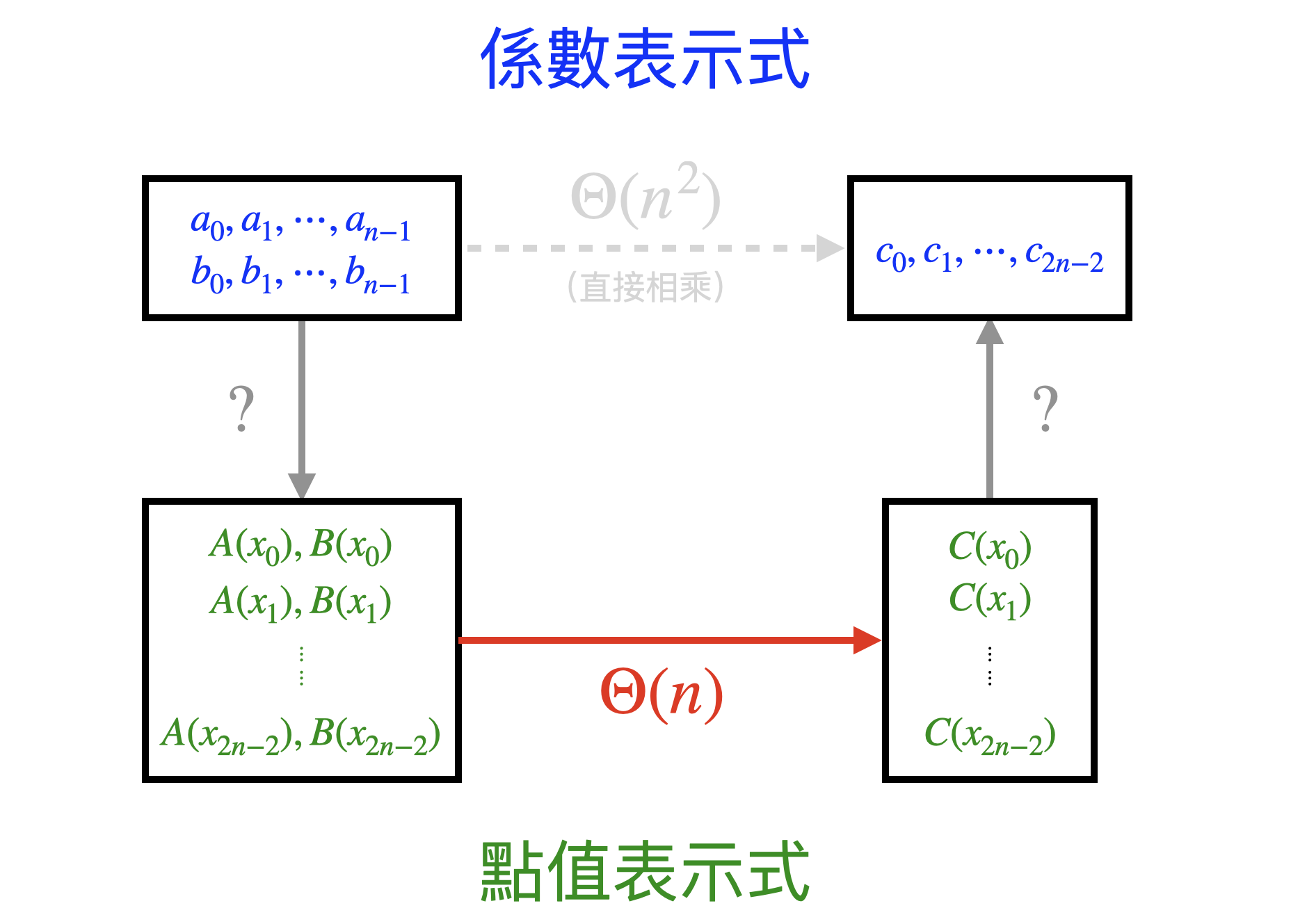
給定 Coefficient Representation，我們現在只會 $O(n\times m)$ 來做多項式乘法。
那如果換成 Point-value Representation 呢？

$C(x_i) = A(x_i) \times B(x_i),~i = 0, 1, \dots, n+m-2$

我們只要能抓 $n+m-1$ 個不同數字的取值，最後一個對一個再相乘起來就好了！只需要 $O(n+m)$ 的時間。

我們可以把計算多項式乘法的任務轉換成：

1. 選擇 $n+m-1$ 個不同的數字 $X=(x_0, x_1, \dots, x_{n+m-2})$
2. 將原本是 Coefficient Representation 的多項式 $A,B$ 轉為 Point-value Representation
3. 在 $O(n+m)$ 的時間計算 $C(x_i) = A(x_i) \times B(x_i)$，得到用 Point-value Representation 表示的多項式 $C$
4. 將多項式 $C$ 轉換回 Coefficient Representation

只要好好的選擇 $X$，就可以用分治法 (divide and conquer) 加速步驟 2, 4。

圖片與文字內容皆參考自 NTHUCPP FFT 單元

$X$ 的選擇

當 $n=2^r,r\ge 0$ 的時候，假設有個 $\omega(n)$ 函數有以下性質：

1. $\omega(n)^0, \omega(n)^1,...,\omega(n)^{n-1}$ 皆為不同數值
2. $\omega(n)^n=1$
3. $\omega(n)^{\frac{n}{2}}=-1$，其實條件 1, 2 同時滿足的話這點會自動成立
4. $\omega(n)^2=\omega(\frac{n}{2})$

設 $$X=(x_0, x_1, \dots, x_{n-1}),~x_i=\omega(n)^i$$ 則原本是 Coefficient Representation 的多項式 $$F(x) := [a_0, a_1, \dots, a_{n - 1}]$$ 其 Point-value Representation $$F(x) := [y_0, y_1, \dots, y_{n - 1}],~y_i=F(x_i)$$

透過 $\omega(n)$ 函數的性質可以利用分治法在 $O(n \log n)$ 的時間遞迴求出來。

若 $n$ 不是 2 的冪次，我們可以找到一個 $n'=2^r,n'>n$，將 $a_n,a_{n+1},...,a_{n'-1}$ 都設為 0，則 $$F'(x)=a_0+a_1x+...+a_{n'-1}x^{n'-1}$$ 就能滿足使用分治法的條件。

分治法 (divide and conquer) 求 Point-value Representation

假設有個函數 $DC(F, n)$ 輸入一個 $n-1$ 次多項式 $F(x)$ 的係數表示法，回傳 $[F(\omega(n)^0), F(\omega(n)^1),..., F(\omega(n)^{n-1})]$。

設 $$\begin{align}
G(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1}\\
H(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}
\end{align}$$ 由 $F$ 的係數得到 $H,G$ 的係數只需要 $O(n)$ 的時間。

我們可以把 $F(x)$ 用 $G(x)$ 和 $H(x)$ 表示：

$$F(x)=G(x^2)+x\times H(x^2)$$ 透過 $DC$ 函數可以遞迴得到 $$\begin{align}
DC(H,n/2)&=[H(\omega(n/2)^0), H(\omega(n/2)^1),..., H(\omega(n/2)^{n/2-1})]\\
DC(G,n/2)&=[G(\omega(n/2)^0), G(\omega(n/2)^1),..., G(\omega(n/2)^{n/2-1})]
\end{align}$$

對於 $0\le k<\frac{n}{2}$，透過性質 2, 3, 4 可以知道：

$\begin{align}
F(\omega(n)^k)&=G(\omega(n)^{2k})+\omega(n)^k\times H(\omega(n)^{2k})\\
&=G(\omega(n/2)^k)+\omega(n)^k\times H(\omega(n/2)^k)\\
\\
F(\omega(n)^{\frac{n}{2}+k})&=G(\omega(n)^{n+2k})+\omega(n)^{\frac{n}{2}+k}\times H(\omega(n)^{n+2k})\\
&=G(\omega(n)^{2k})-\omega(n)^k\times H(\omega(n)^{2k}) \\
&=G(\omega(n/2)^k)-\omega(n)^k\times H(\omega(n/2)^k)
\end{align}$

這樣有了 $DC(H,n/2),DC(G,n/2)$ 就可以在 $O(n)$ 的時間做出 $DC(F,n)$ 的結果。得到遞迴的時間複雜度 $T(n)=O(n) + 2T(n/2) + O(n) = O(n\log n)$。

舉例來說 $n=8$

$F(x)=a_0+a_1x+a_2x^2+...+a_7x^7$

$$\begin{align}
G(x)=a_0+a_2x+a_4x^2+a_6x^3\\
H(x)=a_1+a_3x+a_5x^2+a_7x^3
\end{align}$$

想要用遞迴方法求出 $F(\omega(8)^0), F(\omega(8)^1),..., F(\omega(8)^7)$。

首先可以遞迴求出

$$\begin{align}
G(\omega(4)^0), G(\omega(4)^1), G(\omega(4)^2), G(\omega(4)^3)\\
H(\omega(4)^0), H(\omega(4)^1), H(\omega(4)^2), H(\omega(4)^3)
\end{align}$$

接著可以在 $O(n)$ 得到：

• 用加的
• $F(\omega(8)^0)=G(\omega(4)^0)+\omega(8)^0\times H(\omega(4)^0)$
• $F(\omega(8)^1)=G(\omega(4)^1)+\omega(8)^1\times H(\omega(4)^1)$
• $F(\omega(8)^2)=G(\omega(4)^2)+\omega(8)^2\times H(\omega(4)^2)$
• $F(\omega(8)^3)=G(\omega(4)^3)+\omega(8)^3\times H(\omega(4)^3)$
• 用減的
• $F(\omega(8)^4)=G(\omega(4)^0)-\omega(8)^0\times H(\omega(4)^0)$
• $F(\omega(8)^5)=G(\omega(4)^1)-\omega(8)^1\times H(\omega(4)^1)$
• $F(\omega(8)^6)=G(\omega(4)^2)-\omega(8)^2\times H(\omega(4)^2)$
• $F(\omega(8)^7)=G(\omega(4)^3)-\omega(8)^3\times H(\omega(4)^3)$

程式碼的部分等講完逆變換後在介紹。 

逆變換

設 $(y_0, y_1, \dots, y_{n - 1}),~y_i=F(x_i)$，令多項式 $Z(x)=y_0+y_1x+y_2x^2+y_{n-1}x^{n-1}$，也就是將 $F(x)$ 的 Point-value Representation 作為多項式 $Z(x)$ 的 Coefficient Representation。

將 $\omega(n)^k$ 帶入 $Z(x)$ 可以發現

$$\begin{align}
Z(\omega(n)^k)&=\sum_{i=0}^{n-1} F(\omega(n)^i)\omega(n)^{ik} \\
&=\sum_{i=0}^{n-1} \left(\left(\sum_{j=0}^{n-1} a_j\omega(n)^{ij}\right)\omega(n)^{ik}\right)\\
&=\sum_{j=0}^{n-1}a_j\left(\sum_{i=0}^{n-1} \left(\omega(n)^{j+k}\right)^i\right)
\end{align}$$

這裡等比數列的和只有兩種可能

$$\sum_{i=0}^{n-1} (\omega(n)^{j+k})^i = \left\{
\begin{aligned}
&n&,&~~~j+k\equiv 0\ (mod\ n) \\
&\frac{\omega(n)^{n(j+k)}-1}{\omega(n)^{j+k} -1} = 0&, &~~~\text{else}
\end{aligned}
\right.$$

因此得到結論

1. $Z(\omega(n)^0)=a_0\times n$
2. $Z(\omega(n)^k)=a_{n-k}\times n, ~~~0<k<n$

這表示我們可以將 $y_0\sim y_{n-1}$ 使用同樣的分治法輕鬆地在 $O(n \log n)$ 得到原本多項式 $F(x)$ 的係數 $a_0\sim a_{n-1}$

遞迴版本程式碼

由於我們還不知道 $\omega(n)$ 究竟是個怎樣的函數，實作使用 template 的方式，使用者要將與 $\omega(n)$ 有關的操作寫成 class 後填入 `Policy` 這個欄位。

$\omega(n)$ 的選擇

可以觀察到 $\omega(n)^k$ 有非常明顯的循環性質，這在一般人常見的實數領域中很少見，有這種性質的東西經常出現在：

1. 複數運算的單位根
2. 同餘運算下的有限體 (finite field)

快速傅立葉變換 (Fast Fourier Transform, FFT)

設 $\omega(n)=e^{i\frac{2\pi}{n}}$。透過 Euler's formula 可以知道 $e^{i\frac{2\pi}{n}}=\cos(\frac{2\pi}{n})+i\sin(\frac{2\pi}{n})$

這樣 $\omega(n)$ 的數學含意就是複數的 $n$ 次單位根。

1. $\omega(n)^0, \omega(n)^1,...,\omega(n)^{n-1}$ 的值皆不相同
2. $\omega(n)^n=e^{i\times 2\pi}=1$
3. $\omega(n)^{\frac{n}{2}}=e^{i\pi}=-1$
4. $\omega(n)^2=e^{i\frac{2\times 2\pi}{n}}=e^{i\frac{2\pi}{n/2}}=\omega(\frac{n}{2})$

複數以及 `exp` 函數都是 C++ STL 有提供的東西：

不過使用 FFT 計算多項式乘法會產生浮點數誤差，因此有些人會考慮使用待會會介紹的 FNTT

快速數論變換 (Fast Number-Theoretic Transform, FNTT)

設 $\omega(n)=g^{\frac{P-1}{n}}\mod P$，這裡的 $P$ 是滿足某性質的質數且 $g$ 是$\mod P$ 的原根。因此首先我們要來認識什麼是原根。

什麼是原根

假設 $g, m$ 互質, 使得 $g^d \equiv 1\ (mod\ m)$ 成立的最小正整數 $d$ 定義為 $\delta_m(g)$。

根據歐拉定理 $\delta_m(g)|\phi(m)$，若 $\delta_m(g) = \phi(m)$ ，則稱 $g$ 是$\mod m$ 的原根 (primitive root)。

如果 $m$ 是個質數，則最小的 $g$ 通常是個很小的數字 ($g\ll P^{5/\log\log P}$ by Least Prime Primitive Roots)，zerojudge 上剛好有一題 [b435. 尋找原根]。

對於任意質數 $P>2$ 其原根 $g$ 有一些直觀的性質：

1. $\phi(P)=P-1,~g^{\phi(P)}\equiv g^{P-1}\equiv 1\ (mod\ P)$，這其實就是費馬小定理
2. $g^1,...,g^{P-2},g^{P-1}$ 在$\mod P$ 的結果皆不相同，這是原根本來的性質
3. $g^{(P-1)/2}\equiv -1\ (mod\ P)$ ，由性質 1,2 可以得到

如何選擇質數 $P$

若 $P-1$ 可以被 $n$ 整除，則所有 $\omega(n)$ 的性質都能滿足(所有運算皆是同餘運算)：

1. $\omega(n)^0, \omega(n)^1,...,\omega(n)^{n-1}$ 的值皆不相同
2. $\omega(n)^n=g^{\frac{P-1}{n}n}=g^{P-1}= 1$
3. $\omega(n)^{\frac{n}{2}}=g^{(P-1)/2}=-1$
4. $\omega(n)^2=g^{\frac{2(P-1)}{n}}=g^{\frac{P-1}{n/2}}=\omega(\frac{n}{2})$

為了滿足 $P-1$ 可以被 $n$ 整除，因為 $n$ 是 2 的冪次，FNTT 需要一個特殊構造的質數 $P=r\times 2^k+1,~2^k\ge n$，已經有中國人整理出一些常用的質數：

• 常見的質數 $P=r\times 2^k+1$ 以及其原根 $g$

$P=998244353=7\times 17\times 2^{23}+1$ 是個經常被使用的質數，其原根 $g=3$。

這樣我們就可以輕鬆地根據定義寫出 FNTT 的實作：

注意 FNTT 的所有運算皆是同餘運算，也就是說 FNTT 的計算多項式乘法的結果是原本的數字$\mod P$ 的值，因此若需要得到精確的結果需要用不同質數執行多次 FNTT 使用中國剩餘定理將結果合併。

假設有個 $n-1$ 次多項式要和一個 $m-1$ 次多項式做乘法，這兩個多項式的所有係數皆小於一個正整數 $q$。

那麼這樣任何多項式係數的範圍就是 $[0,q-1]$，係數兩兩相乘不會超過 $(q-1)^2$，一共最多 $\min(n,m)$ 項相加，不會超過 $\min(n,m)\times(q-1)^2$。

我們可以選 $k$ 個可以進行 FNTT 的不同質數使得以下條件成立：

$$\prod_{i=1}^{k}p_i>\min(n,m)\times(q-1)^2$$

這樣分別使用這些質數執行 FNTT 後再使用中國剩餘定理將結果合併就可以得到完全精確的係數，但要注意計算範圍可能會超過 `long long`，甚至有可能會需要 `__int128_t`。

非遞迴版 Cooley-Tukey Algorithm

我們將係數遞迴的狀況畫出來，注意到葉節點係數的順序會是 $(0, 4, 2, 6, 1, 5, 3, 7)$：

觀察這棵樹，由上往下的第 $i$ 次分層時，是按照其 index 在第 $i$ 個 bit 的奇偶分兩邊的，並且第 $i$ 次分層會決定其最後位子的第 $\log_2 n - i - 1$ 個 bit。

可以推論出，index $i$ 的換置後的位子就會將是 $i$ 的 binary representation 給 reverse。

Reverse Bit 的方法

遞推建表法，建立 $O(n)$ 大小表，總時間複雜度也是 $O(n)$

直接換置法，一次反轉一個數字 $n$，只要 $O(1)$ 空間，但時間複雜度是 $O(\log\log n)$

如果 index $i$ 的位置是 $j$，那麼 index $j$ 的位置也會是 $i$。

想要節省空間的話，可以考慮用直接換置法 in-place 進行換置：

蝶形網路 Butterfly Diagram

我們一開始就把係數的順序透過 bit reverse 換置，可以寫出非遞迴版本的程式碼：

將計算流程畫成圖形，可以看到有很多長得像蝴蝶的形狀，因此被稱之為蝶形網路：

離散捲積程式碼

測試程式碼

Output:

5 16 34 60 70 70 59 36
(5.0,0.0) (16.0,0.0) (34.0,0.0) (60.0,-0.0) (70.0,-0.0) (70.0,-0.0) (59.0,-0.0) (36.0,0.0)
5 16 34 60 70 70 59 36 

[Counting Sort, Radix Sort] 計數排序, 基數排序

 Counting Sort是一種效率很高的排序方式，複雜度為$\ord{n+k}$，其中$k$是Bucket的大小，由此可知僅限於整數且數字範圍不能太大。根據觀察在很多應用中會有對物件以編號大小進行排序的行為，在這方面應該能做到很大的加速。

另外一個問題是Counting Sort雖然簡單，很多人甚至可以自己想到實作方法，但這也導致了標準的作法常常被人忽略。因此這裡就來給大家展示標準的Counting sort：

參數的解釋如下：

• First, Last:
  和std::sort的定義一樣，需要排序的範圍，注意不一定要是random access iterator。
• BucketFirst, BucketLast:
  Counting Sort正統的實作方式會有一個正整數陣列作為Bucket，考量到各種應用所以這裡接傳Bucket的範圍進來能做的優化會比較多，必須要是random access iterator。
• OutputFirst:
  Counting Sort的output是直接將input存到另一個陣列中，因此OutputFirst指的是Output陣列的開頭，必須要是random access iteator，且要注意output的空間是足夠的。這邊將input存進output時是用std::move的方式，如果想要保留原本input的話可以將其拿掉。
• Key:
  這是一個函數，Key(x)必須要回傳一個0~(BucketLast-BucketFirst-1)的正整數作為被排序物件x的關鍵值。

有了Counting sort，Radix Sort就比較好解釋了。首先正統的Counting sort是stable sort，所以Key值相同的東西排序前後的先後順序是不變的。因此可以透過多次的Counting Sort來完成一些原本Counting Sort無法完成的事情。

以整數(int, -2147483648~2147483647)排序為例，可以先針對第十億位做為Key進行排序，接著再對第一億位做為Key、第一千萬位做為Key...直到十位數、個位數作為Key，最後再以正負號最為Key進行排序，這樣就可以完成一般範圍的整數排序。

實際上一般不會這樣用，通常是用在有多個Key值的情況，以下面的程式碼來說，可以自行執行看看花費的時間有多少：

[Discretize Relabeling] 離散化器

離散化是演算法競賽常用的操作，在各種實際問題上也能看到其應用。最基本的情況，是對於n個可排序的元素，製造一個map使得它們可以和自己的名次一一對應，但通常的應用中這n個元素確定之後就不太會有增減的動作，因此可以存到vector中排序去除重複的部分，搜索的部分就用二分搜尋來取代。

[Multiple line segment intersection] Bentley–Ottmann 演算法

 基本上這個問題就是給你一些線段(格式通常為兩個端點)，你要找出這些線段的交點。直觀的做法兩兩進行計算會花上$\ord{n^2}$的時間，但大多數的情況下交點不會很多。為了解決這個問題，修改自Shamos–Hoey演算法的Bentley–Ottmann演算法可以在$\ord{(n+k)\log n}$的時間內找出所有交點，其中$k$是交點數量。

這裡附上實作時需要用到的基本資料結構：

演算法使用掃描線進行。掃描線是一條垂直線從左邊掃到右邊(有些實作是水平線從上面掃到下面)，並且在遇到事件點的時候進行相關處理。

線段的兩端點以及交點都作為事件點被紀錄在最終結果中。對於每個事件點$P$，我們會計算三個集合：

• U集合：所有以$P$為起始點的線段集合
• C集合：所有包含$P$的線段集合
• L集合：所有以$P$為結束點的線段集合

當然要先保證每條線段的起始點移動會在結束點的左方，只要得到線段後稍微判斷一下就可以做到了。每個事件點找出這三個集合後就可以很容易的判斷相交資訊，但要注意的是會有以下的退化情形：

• 線段退化成點：這種情況該點的U和L都會包含該線段。
• 兩線段重合：只有重合處的兩端點會被紀錄為事件點，可以根據UCL判斷出是否線段重合
• 垂直線段：排序點和線段時如果x一樣就按照y來比較
  

最後是掃描線的資料結構，需要一棵平衡的BST根據當前掃描線和各個線段切點的y值進行排序，但這件事是可以用STL做到的！我們把當前事件點傳進比較函數裡面進行計算，因為在任何一個時刻BST中的資料都是根據當前的比較函數由小排到大的，應該不算undefined behavior。另外該演算法的浮點數誤差很大，建議使用時套上處理誤差的模板或是直接用分數計算：

最後是測試的部分，以下圖做為測試範例：

將該圖轉換成我們接受的input如下：

10

-2 7 2 0

-2 7 -2 0

-2 6 2 5

-2 6 2 2

-2 4 2 7

-2 4 2 2

-2 4 4 1

-2 0 2 2

0 1 0 1

0 3 4 1

最後附上測試程式碼，需要的話可以自己執行看看：

[ Minimum Spanning Tree, kruskal, prim ] 最小生成樹經典演算法

以前覺得這應該是很簡單的東西，但我發現網路上使用priority_queue的prim演算法相關程式碼我覺得寫不好，我就把我自己的放上來。這裡順便也放上kruskal的程式碼。

prim $\ord{\left(\abs{V}+\abs{E}\right)\log{\abs{V}}}$:
kruskal $\ord{\abs{V}+\abs{E}\log{\abs{E}}}$:

[ Delaunay Triangulation ] Delaunay 三角剖分

我高中的時候在morris的網站第一次看到這個東西，那個時候就很想試著寫出來看看，但那時候英文很不好所以不會找資料就沒有成功。直到今年的NPSC，聽說台大出了一題找Voronoi Diagram的題目沒有人寫出來，於是我就想挑戰看看，寒假開始之後就認真研讀相關資料，終於在前幾天完成了隨機增量法以及分治法的模板。

先來說說甚麼是三角剖分 Triangulation 吧！假設平面上散布很多不重複的點，現在用一些線段將這些點連成許多的三角形，滿足所有三角形的內部不會有其他點，而且三角形的數量越多越好，這就是一個三角剖分。

Delaunay Triangulation是一種特殊的三角剖分，滿足所有的三角形其外接圓中不會出現其他的點，這樣的性質會使得所有三角形中最小的角盡量大，而且最重要的是它是 Voronoi Diagram 的對偶圖，Voronoi Diagram 直接求的話很容易有浮點誤差而且程式也不好寫，因此從Delaunay Triangulation直接轉換過去會更加方便。

還有一個很重要的點，透過Delaunay Triangulation 的邊集合可以找出平面歐幾里得距離最小生成樹。

這裡我先給出點的資料結構，方便接下來的講解：

一般來說找出 Delaunay Triangulation 的其中一個操作是要判斷一個點是不是在一個三角形的外接圓內，但直接去求外接圓圓心會有浮點誤差，因此有一個作法是將所有點投影到三維的拋物線曲面中，也就是下圖的碗狀曲面，會發現把一個圓投影上去之後，該圓會落在一個平面上，圓內的點會在平面下面，圓外的點會在平面上面，這樣就可以利用一些處理三維幾何的技術就可以避免浮點誤差的判斷點是否在外接圓內了。

範例程式碼中點在圓內輸出1，圓外輸出-1，圓上輸出0：

當然實作時並不會真正的寫一個三維點的資料結構，這樣程式碼會比較長。

Delaunay Triangulation 我所知道的有兩種，分別是隨機增量法以及分治法。隨機增量法再點隨機加入的時候複雜度是$\ord{n\log n}$，分治法則是穩定$\ord{n\log n}$，但我的實作分治法的效能是隨機增量法的三倍快。由於兩種做法都已經有詳細教學了這裡就不用文字敘述。

1. 隨機增量法教學在《Computational Geometry - Algorithms and Applications》書中有提到，該書有中文版
2. 分治法教學請點該網站連結

這裡附上程式碼，順帶一提morris的分治法好像在某些測資會因為三點共線爛掉

隨機增量法：

分治法：